Einstein Coefficient Relation derivation and discussion:
Einstein showed the interaction of radiation with the matter with the help of three processes called stimulated absorption, spontaneous emission, and stimulated emission. He showed in 1917 that for a proper description of radiation with matter, the process of stimulated emission is essential. Let us first derive the Einstein coefficient relation on the basis of the above theory:

Let N₁ be the number of atoms per unit volume in the ground state E₁ and these atoms exist in the radiation field of photons of energy E₂-E₁ =h v such that the energy density of the field is E.

Einstein Coefficient for Stimulated Absorption:

Let R₁ be the rate of absorption of light by E₁ -> E₂ transitions by the process called stimulated absorption (Refer below figure):

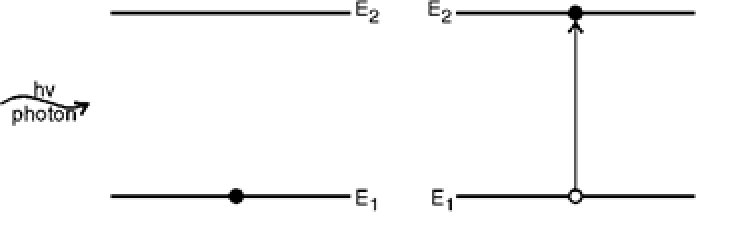
This rate of absorption R₁ is proportional to the number of atoms N₁ per unit volume in the ground state and proportional to the energy density E of radiations.

That is                                    R₁∞ N₁ E

Or                                          R₁ = B₁₂N₁ E                                               (1)

Where B₁₂ is known as the Einstein’s coefficient of stimulated absorption and it represents the probability of absorption of radiation. Energy density e is defined as the incident energy on an atom as per unit volume in a state.

Einstein Coefficient for Spontaneous Emission:

Now atoms in the higher energy level E₂ can fall to the ground state E₁ automatically after 10^-8 sec by the process called spontaneous emission (Refer below figure).

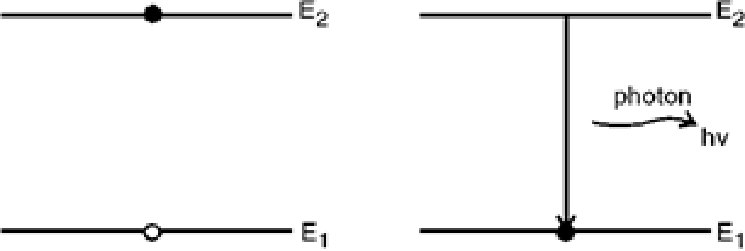
The rate R₂ of spontaneous emission E₂-> E₁ is independent of energy density E of the radiation field.

R₂ is proportional to number of atoms N₂ in the excited state E₂ thus

R₂∞ N₂

R₂=A₂₁ N₂ (2)

Where A₂₁ is known as Einstein’s coefficient for spontaneous emission and it represents the probability of spontaneous emission.

Einstein Coefficient for Stimulated Emission:

Atoms can also fall back to the ground state E₁ under the influence of the electromagnetic field of an incident photon of energy E₂-E₁ =hv by the process called stimulated emission (Refer below Figure):

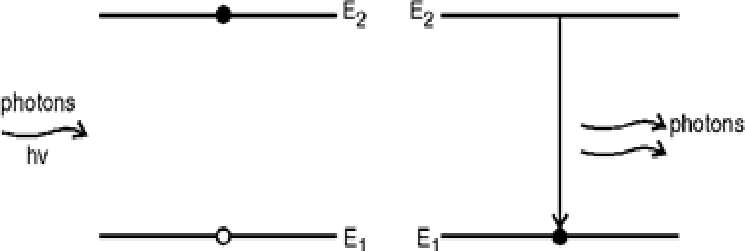
Rate R₃ for stimulated emission E₂-> E_1­ is proportional to energy density E of the radiation field and proportional to the number of atoms N₂ in the excited state,thus

R₃α N₂ E

Or                   R₃=B₂₁N₂ E                                                       (3)

Where B₂₁ is known as the Einstein coefficient for stimulated emission and it represents the probability of stimulated emission.

Einstein Coefficient Relation Derivation:

In steady-state (at thermal equilibrium), the two emission rates (spontaneous and stimulated) must balance the rate of absorption.

Thus                                                         R₁=R₂+R₃

Using equations (1,2, and 3) ,we get

N₁B₁₂E=N₂A₂₁+N₂B₂₁E

Or            N₁B₁₂E –N₂B₂₁E=N₂A₂₁

Or         (N₁B₁₂-N₂B₂₁) E =N₂A₂₁

Or           E= N₂A₂₁/N₁B₁₂-N₂B₂₁

= N₂A₂₁/N₂B₂₁[N₁B₁₂/N₂B₂₁ -1]

[by taking out common N₂B₂₁from the denominator]

Or                        E=A₂₁/B₂₁ {1/N₁/N₂(B₁₂/B₂₁-1))                                         (4)

Einstein proved thermodynamically, that the probability of stimulated absorption is equal to the probability of stimulated emission. thus

B₁₂=B₂₁

Then equation(4) becomes

E=A₂₁/B₂₁(1/N₁/N₂-1)                                                       (5)

From Boltzman’s distribution law, the ratio of populations of two levels at temperature T is expressed as

N₁/N₂=e^(E₂–^E₁^)/KT

N₁/N₂=e^hv/KT

Where K is the Boltzman’s constant and h is Planck’s constant.

Substituting value of N₁/N₂in equation (5) we get

E=  A₂₁/B₂₁(1/e^hv/KT-1)                                                        (6)

Now according to Planck’s radiation law, the energy density of the black body radiation of frequency v at temperature T is given as

E =    8πhv³/c³(1/e^hv/KT)                                                                  (7)

By comparing equations (6 and 7),we get

A₂₁/B₂₁=8πhv³/c³

This is the relation between Einstein’s coefficients in laser.

Significance of Einstein coefficient relation: This shows that the ratio of Einstein’s coefficient of spontaneous emission to the Einstein’s coefficient of stimulated absorption is proportional to the cube of frequency v. It means that at thermal equilibrium, the probability of spontaneous emission increases rapidly with the energy difference between two states. If you want to learn derivation of Einstein Coefficient relations, then following is our youtube video also: